Dlaczego większość opublikowanych wyników badań jest fałszywa – prof. John Ioannidis
Źródło: PLoS Med. 2005 Aug; 2(8): e124; Why Most Published Research Findings Are False

Myślenie pojęciowe, a myślenie stereotypowe – Andrzej Wronka, Kazimierz Ajdukiewicz, Józef Kossecki
O tworzeniu pojęć klasowych oraz teoriach adekwatnych, kulawych i skaczących – Leon Petrażycki
Istnieją coraz większe obawy, że większość obecnie publikowanych wyników badań jest fałszywa. Prawdopodobieństwo, że twierdzenie badawcze jest prawdziwe, może zależeć od mocy i stronniczości badania, liczby innych badań dotyczących tego samego pytania oraz, co ważne, stosunku prawdziwych do nieprawdziwych relacji wśród relacji badanych w każdej dziedzinie naukowej. W tym ujęciu prawdopodobieństwo prawdziwości wyników badań jest mniejsze, gdy badania przeprowadzone w danej dziedzinie są mniejsze; gdy rozmiary efektów są mniejsze; gdy istnieje większa liczba i mniejsza preselekcja badanych związków; gdy istnieje większa elastyczność w projektach, definicjach, wynikach i trybach analitycznych; gdy istnieje większe zainteresowanie finansowe i inne oraz uprzedzenia; oraz gdy więcej zespołów jest zaangażowanych w daną dziedzinę naukową w pogoni za istotnością statystyczną. Symulacje pokazują, że w przypadku większości projektów badań i ustawień bardziej prawdopodobne jest, że twierdzenie badawcze będzie fałszywe niż prawdziwe. Co więcej, w przypadku wielu obecnych dziedzin naukowych, deklarowane wyniki badań mogą często być po prostu dokładnymi miarami dominującego uprzedzenia. W tym eseju omawiam implikacje tych problemów dla prowadzenia i interpretacji badań.
Opublikowane wyniki badań są czasami obalane przez kolejne dowody, mówi John Ioannidis, powodując zamieszanie i rozczarowanie.
Opublikowane wyniki badań są czasami obalane przez kolejne dowody, co powoduje zamieszanie i rozczarowanie. Obalanie i kontrowersje są widoczne w całym zakresie projektów badawczych, od badań klinicznych i tradycyjnych badań epidemiologicznych[1-3] po najnowocześniejsze badania molekularne[4,5]. Istnieją coraz większe obawy, że w nowoczesnych badaniach fałszywe wyniki mogą stanowić większość lub nawet zdecydowaną większość opublikowanych twierdzeń badawczych[6-8]. Nie powinno to jednak dziwić. Można udowodnić, że większość twierdzeń badawczych jest fałszywa. W tym miejscu przeanalizuję kluczowe czynniki, które wpływają na ten problem i niektóre jego następstwa.
Modelowanie ram dla wyników fałszywie pozytywnych
Kilku metodologów wskazało[9-11], że wysoki wskaźnik braku replikacji (braku potwierdzenia) odkryć badawczych jest konsekwencją wygodnej, ale nieuzasadnionej strategii twierdzenia o rozstrzygających wynikach badań wyłącznie na podstawie pojedynczego badania ocenianego na podstawie formalnej istotności statystycznej, zwykle dla wartości p mniejszej niż 0,05. Badania nie są najlepiej reprezentowane i podsumowywane przez wartości p, ale niestety istnieje powszechne przekonanie, że artykuły z badań medycznych powinny być interpretowane wyłącznie na podstawie wartości p. Wyniki badań są tutaj definiowane jako wszelkie relacje osiągające formalną istotność statystyczną, np. skuteczne interwencje, predyktory informacyjne, czynniki ryzyka lub powiązania. Badania „negatywne” są również bardzo przydatne. „Negatywne” to w rzeczywistości błędne określenie, a błędna interpretacja jest szeroko rozpowszechniona. Jednak w tym przypadku będziemy koncentrować się na związkach, które według badaczy istnieją, a nie na wynikach zerowych.
05/03/2019: How to Hack P-Values: A User’s Guide
Można udowodnić, że większość twierdzeń badawczych jest fałszywa
Jak wykazano wcześniej, prawdopodobieństwo, że odkrycie badawcze jest rzeczywiście prawdziwe, zależy od wcześniejszego prawdopodobieństwa jego prawdziwości (przed przeprowadzeniem badania), mocy statystycznej badania i poziomu istotności statystycznej[10,11]. Rozważmy tabelę 2 × 2, w której wyniki badań są porównywane ze złotym standardem prawdziwych relacji w dziedzinie nauki. W dziedzinie badań można postawić zarówno prawdziwe, jak i fałszywe hipotezy dotyczące obecności związków. Niech R będzie stosunkiem liczby „prawdziwych relacji” do „braku relacji” wśród badanych w danej dziedzinie. R jest charakterystyczne dla danej dziedziny i może się znacznie różnić w zależności od tego, czy dana dziedzina jest ukierunkowana na wysoce prawdopodobne relacje, czy też szuka tylko jednej lub kilku prawdziwych relacji wśród tysięcy lub milionów hipotez, które mogą być postulowane. Rozważmy również, dla uproszczenia obliczeniowego, ograniczone pola, w których albo istnieje tylko jeden prawdziwy związek (spośród wielu, które można postawić), albo moc jest podobna do znalezienia dowolnego z kilku istniejących prawdziwych związków. Prawdopodobieństwo prawdziwości związku przed badaniem wynosi R/(R + 1). Prawdopodobieństwo znalezienia prawdziwego związku w badaniu odzwierciedla moc 1 – β (jeden minus poziom błędu typu II). Prawdopodobieństwo stwierdzenia związku, gdy żaden naprawdę nie istnieje, odzwierciedla poziom błędu typu I, α. Zakładając, że w terenie badane są relacje c, oczekiwane wartości tabeli 2 × 2 podano w tabeli 1. Po stwierdzeniu odkrycia badawczego w oparciu o osiągnięcie formalnej istotności statystycznej, prawdopodobieństwo po badaniu, że jest ono prawdziwe, jest pozytywną wartością predykcyjną (positive predictive value – PPV). Pozytywna wartość predykcyjna jest również uzupełniającym prawdopodobieństwem tego, co Wacholder i in. nazwali prawdopodobieństwem fałszywie dodatniego raportu[10]. Zgodnie z tabelą 2 × 2 otrzymujemy PPV = (1 – β)R/(R – βR + α). Odkrycie badawcze jest zatem bardziej prawdopodobne, że jest prawdziwe niż fałszywe, jeśli (1 – β)R > α. Ponieważ zwykle zdecydowana większość badaczy polega na a = 0,05, oznacza to, że odkrycie badawcze jest bardziej prawdopodobne, że jest prawdziwe niż fałszywe, jeśli (1 – β)R > 0,05.
Tabela 1

To, co jest mniej doceniane, to fakt, że stronniczość i zakres powtarzających się niezależnych testów przeprowadzanych przez różne zespoły badaczy na całym świecie mogą dodatkowo zniekształcać ten obraz i prowadzić do jeszcze mniejszego prawdopodobieństwa, że wyniki badań są rzeczywiście prawdziwe. Spróbujemy modelować te dwa czynniki w kontekście podobnych tabel 2 × 2.
Stronniczość
Po pierwsze, zdefiniujmy stronniczość jako połączenie różnych czynników związanych z projektem, danymi, analizą i prezentacją, które mają tendencję do generowania wyników badań, gdy nie powinny one być generowane. Niech u będzie odsetkiem badanych analiz, które nie byłyby „wynikami badań”, ale mimo to zostały przedstawione i zgłoszone jako takie z powodu stronniczości. Stronniczości nie należy mylić ze zmiennością przypadkową, która powoduje, że niektóre wyniki są fałszywe przez przypadek, nawet jeśli projekt badania, dane, analiza i prezentacja są doskonałe. Stronniczość może wiązać się z manipulacją w analizie lub raportowaniu wyników. Typową formą takiej stronniczości jest selektywne lub zniekształcone raportowanie. Możemy założyć, że u nie zależy od tego, czy prawdziwy związek istnieje, czy nie. Nie jest to nieuzasadnione założenie, ponieważ zazwyczaj nie można wiedzieć, które relacje są rzeczywiście prawdziwe. W obecności błędu systematycznego (Tabela 2), otrzymujemy PPV = ([1 – β]R + uβR)/(R + α – βR + u – uα + uβR), a pozytywna wartość predykcyjna [PPV] maleje wraz ze wzrostem u, chyba że 1 – β ≤ α, tj. 1 – β ≤ 0,05 w większości sytuacji. Tak więc, wraz ze wzrostem błędu systematycznego, szanse na to, że wyniki badań są prawdziwe, znacznie maleją. Jest to pokazane dla różnych poziomów mocy i różnych kursów przed badaniem na rycinie 1. Z drugiej strony, prawdziwe wyniki badań mogą być czasami anulowane z powodu odwrotnej tendencyjności. Na przykład przy dużych błędach pomiarowych relacje są tracone w szumie[12] lub badacze wykorzystują dane nieefektywnie lub nie zauważają statystycznie istotnych relacji, lub mogą istnieć konflikty interesów, które mają tendencję do „zakopywania” istotnych ustaleń[13]. Nie ma dobrych dowodów empirycznych na dużą skalę na to, jak często taka odwrotna tendencyjność może występować w różnych dziedzinach badań. Prawdopodobnie można jednak stwierdzić, że odwrotna tendencyjność nie jest tak powszechna. Co więcej, błędy pomiarowe i nieefektywne wykorzystanie danych prawdopodobnie stają się coraz rzadszymi problemami, ponieważ błąd pomiarowy zmniejszył się wraz z postępem technologicznym w erze molekularnej, a badacze stają się coraz bardziej wyrafinowani w zakresie swoich danych. Niezależnie od tego, błąd odwrotny może być modelowany w taki sam sposób, jak błąd odwrotny opisany powyżej. Odwrotnej tendencyjności nie należy również mylić ze zmiennością przypadkową, która może prowadzić do przeoczenia prawdziwego związku z powodu przypadku.
Rycina 1
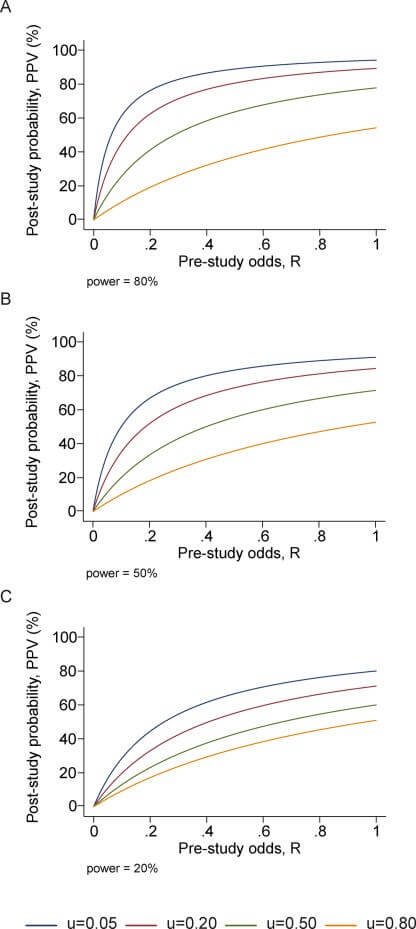
PPV (prawdopodobieństwo, że wyniki badania są prawdziwe) jako funkcja szans przed badaniem dla różnych poziomów błędu systematycznego, u; Panele odpowiadają mocy 0,20, 0,50 i 0,80.
Tabela 2
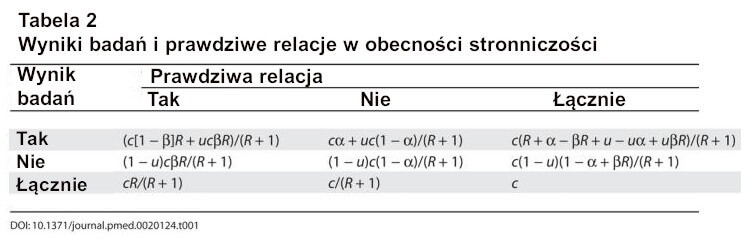
Testowanie przez kilka niezależnych zespołów
Kilka niezależnych zespołów może zajmować się tymi samymi zestawami pytań badawczych. Wraz z globalizacją wysiłków badawczych, praktycznie regułą jest, że kilka zespołów badawczych, często dziesiątki, może badać te same lub podobne pytania. Niestety, w niektórych obszarach dominującą mentalnością do tej pory było skupianie się na pojedynczych odkryciach dokonywanych przez pojedyncze zespoły i interpretowanie eksperymentów badawczych w izolacji. Coraz więcej pytań ma co najmniej jedno badanie, które twierdzi, że jest odkryciem badawczym, i jest ono przedmiotem jednostronnej uwagi. Prawdopodobieństwo, że co najmniej jedno badanie, spośród kilku przeprowadzonych na to samo pytanie, twierdzi, że jest statystycznie istotne, jest łatwe do oszacowania. Dla n niezależnych badań o równej mocy, tabela 2 × 2 jest pokazana w tabeli 3: PPV = R(1 – βn)/(R + 1 – [1 – α]n – Rβn) (bez uwzględnienia stronniczości). Wraz ze wzrostem liczby niezależnych badań PPV ma tendencję do zmniejszania się, chyba że 1 – β < a, tj. zazwyczaj 1 – β < 0,05. Pokazano to dla różnych poziomów mocy i dla różnych kursów przed badaniem na rycienie 2. W przypadku n badań o różnej mocy termin βn jest zastępowany iloczynem terminów βi dla i = 1 do n, ale wnioski są podobne.
Rycina 2
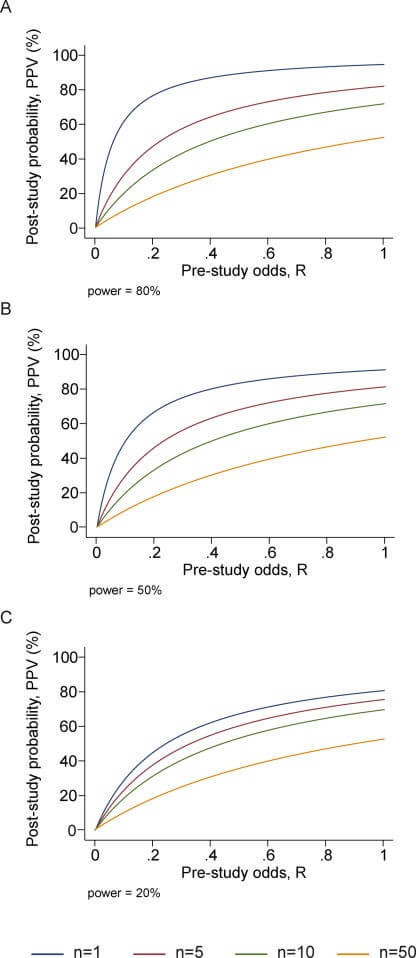
PPV (prawdopodobieństwo, że wyniki badania są prawdziwe) jako funkcja szans przed badaniem dla różnej liczby przeprowadzonych badań, n; Panele odpowiadają mocy 0,20, 0,50 i 0,80.

Następstwa
Praktyczny przykład pokazano w ramce 1. Na podstawie powyższych rozważań można wydedukować kilka interesujących wniosków dotyczących prawdopodobieństwa, że odkrycie badawcze jest rzeczywiście prawdziwe.
Ramka 1. Przykład: Nauka z niskim prawdopodobieństwem przed badaniem
Załóżmy, że zespół badaczy przeprowadza badanie asocjacyjne całego genomu w celu sprawdzenia, czy którykolwiek ze 100.000 polimorfizmów genowych jest związany z podatnością na schizofrenię. Opierając się na tym, co wiemy o stopniu dziedziczności choroby, rozsądne jest oczekiwanie, że prawdopodobnie około dziesięciu polimorfizmów genowych spośród testowanych będzie rzeczywiście związanych ze schizofrenią, przy stosunkowo podobnych ilorazach szans około 1.3 dla około dziesięciu polimorfizmów i przy dość podobnej mocy do zidentyfikowania któregokolwiek z nich. Wtedy R = 10/100,000 = 10-4, a prawdopodobieństwo przed badaniem, że jakikolwiek polimorfizm będzie związany ze schizofrenią wynosi również R/(R + 1) = 10-4. Załóżmy również, że badanie ma 60% mocy, aby znaleźć związek z ilorazem szans 1.3 przy α = 0,05. Następnie można oszacować, że jeśli statystycznie istotny związek zostanie znaleziony przy wartości p ledwo przekraczającej próg 0,05, prawdopodobieństwo po badaniu, że jest to prawda, wzrasta około 12-krotnie w porównaniu z prawdopodobieństwem przed badaniem, ale nadal wynosi tylko 12 × 10-4.
Załóżmy teraz, że badacze manipulują swoim projektem, analizami i raportowaniem, aby więcej relacji przekroczyło próg p = 0,05, mimo że nie zostałby on przekroczony przy doskonale przestrzeganym projekcie i analizie oraz przy doskonałym kompleksowym raportowaniu wyników, ściśle według oryginalnego planu badania. Takich manipulacji można dokonać na przykład poprzez przypadkowe włączenie lub wykluczenie niektórych pacjentów lub kontroli, analizy podgrup post hoc, badanie kontrastów genetycznych, które nie zostały pierwotnie określone, zmiany w definicjach choroby lub kontroli oraz różne kombinacje selektywnego lub zniekształconego raportowania wyników. Dostępne na rynku pakiety „eksploracji danych” są w rzeczywistości dumne ze swojej zdolności do uzyskiwania statystycznie istotnych wyników poprzez pogłębianie danych. W obecności błędu systematycznego przy u = 0,10, prawdopodobieństwo, że wyniki badania po jego zakończeniu są prawdziwe, wynosi tylko 4,4 × 10-4. Co więcej, nawet przy braku jakiejkolwiek stronniczości, gdy dziesięć niezależnych zespołów badawczych przeprowadza podobne eksperymenty na całym świecie, jeśli jeden z nich znajdzie formalnie statystycznie istotne powiązanie, prawdopodobieństwo, że odkrycie badawcze jest prawdziwe, wynosi tylko 1,5 × 10-4, czyli niewiele więcej niż prawdopodobieństwo, które mieliśmy przed podjęciem jakichkolwiek z tych szeroko zakrojonych badań!
Następstwo 1: Im mniejsza liczba badań przeprowadzonych w danej dziedzinie naukowej, tym mniejsze prawdopodobieństwo, że wyniki badań są prawdziwe. Mały rozmiar próby oznacza mniejszą moc, a dla wszystkich powyższych funkcji PPV dla prawdziwych wyników badań maleje wraz ze spadkiem mocy w kierunku 1 – β = 0,05. Tak więc, przy innych czynnikach równych, wyniki badań są bardziej prawdopodobne w dziedzinach naukowych, które podejmują duże badania, takie jak randomizowane badania kontrolowane w kardiologii (kilka tysięcy osób poddanych randomizacji)[14] niż w dziedzinach naukowych z małymi badaniami, takimi jak większość badań nad predyktorami molekularnymi (wielkość próby 100-krotnie mniejsza)[15].
Następstwo 2: Im mniejsza wielkość efektu w danej dziedzinie naukowej, tym mniejsze prawdopodobieństwo, że wyniki badań są prawdziwe. Moc jest również związana z wielkością efektu. Tak więc wyniki badań są bardziej prawdopodobne w dziedzinach naukowych o dużych efektach, takich jak wpływ palenia tytoniu na raka lub choroby układu krążenia (ryzyko względne 3-20), niż w dziedzinach naukowych, w których postulowane efekty są małe, takie jak genetyczne czynniki ryzyka chorób multigenetycznych (ryzyko względne 1,1-1,5)[7]. Współczesna epidemiologia jest coraz bardziej zobowiązana do osiągania mniejszych rozmiarów efektów[16]. W związku z tym oczekuje się, że odsetek prawdziwych wyników badań zmniejszy się. Zgodnie z tym samym tokiem myślenia, jeśli prawdziwe rozmiary efektu są bardzo małe w danej dziedzinie naukowej, dziedzina ta może być nękana przez niemal wszechobecne fałszywie pozytywne twierdzenia. Na przykład, jeśli większość prawdziwych genetycznych lub żywieniowych determinantów złożonych chorób wiąże się z ryzykiem względnym mniejszym niż 1.05, epidemiologia genetyczna lub żywieniowa byłaby w dużej mierze utopijnym przedsięwzięciem.
Następstwo 3: Im większa liczba i mniejsza selekcja testowanych związków w danej dziedzinie naukowej, tym mniejsze prawdopodobieństwo, że wyniki badań są prawdziwe. Jak pokazano powyżej, prawdopodobieństwo prawdziwości odkrycia po badaniu (PPV) zależy w dużej mierze od prawdopodobieństwa przed badaniem (R). W związku z tym wyniki badań są bardziej prawdopodobne w projektach potwierdzających, takich jak duże randomizowane kontrolowane badania III fazy lub ich metaanalizy, niż w eksperymentach generujących hipotezy. Dziedziny uważane za wysoce informacyjne i kreatywne, biorąc pod uwagę bogactwo zgromadzonych i przetestowanych informacji, takie jak mikromacierze i inne wysokoprzepustowe badania zorientowane na odkrycia[4,8,17], powinny mieć wyjątkowo niskie PPV.
Następstwo 4: Im większa elastyczność w projektach, definicjach, wynikach i trybach analitycznych w danej dziedzinie nauki, tym mniejsze prawdopodobieństwo, że wyniki badań będą prawdziwe. Elastyczność zwiększa potencjał przekształcania „negatywnych” wyników w „pozytywne”, tj. stronniczość, u. W przypadku kilku projektów badawczych, np. randomizowanych badań kontrolowanych[18-20] lub metaanaliz[21,22], podjęto wysiłki w celu standaryzacji ich prowadzenia i raportowania. Przestrzeganie wspólnych standardów prawdopodobnie zwiększy odsetek prawdziwych wyników. To samo dotyczy wyników. Prawdziwe wyniki mogą być bardziej powszechne, gdy wyniki są jednoznaczne i powszechnie uzgodnione (np. śmierć), niż gdy opracowywane są różnorodne wyniki (np. skale wyników schizofrenii)[23]. Podobnie, dziedziny, które wykorzystują powszechnie uzgodnione, stereotypowe metody analityczne (np. wykresy Kaplana-Meiera i test log-rank)[24] mogą dawać większy odsetek prawdziwych wyników niż dziedziny, w których metody analityczne są nadal eksperymentowane (np. metody sztucznej inteligencji) i zgłaszane są tylko „najlepsze” wyniki. Niezależnie od tego, nawet w najbardziej rygorystycznych projektach badawczych, stronniczość wydaje się być poważnym problemem. Na przykład, istnieją mocne dowody na to, że selektywne raportowanie wyników, wraz z manipulacją wynikami i analizami, jest powszechnym problemem nawet w przypadku randomizowanych badań[25]. Samo zniesienie selektywnej publikacji nie sprawi, że problem ten zniknie.
Następstwo 5: Im większe finansowe i inne interesy oraz uprzedzenia w danej dziedzinie nauki, tym mniejsze prawdopodobieństwo, że wyniki badań są prawdziwe. Konflikty interesów i uprzedzenia mogą zwiększać stronniczość, u. Konflikty interesów są bardzo powszechne w badaniach biomedycznych[26] i zazwyczaj są nieodpowiednio i rzadko zgłaszane[26,27]. Uprzedzenia niekoniecznie muszą mieć podłoże finansowe. Naukowcy w danej dziedzinie mogą być uprzedzeni wyłącznie z powodu wiary w teorię naukową lub zaangażowania we własne odkrycia. Wiele pozornie niezależnych badań uniwersyteckich może być prowadzonych wyłącznie w celu zapewnienia lekarzom i badaczom kwalifikacji do awansu lub zatrudnienia. Takie niefinansowe konflikty mogą również prowadzić do zniekształconych wyników i interpretacji. Prestiżowi badacze mogą tłumić poprzez proces wzajemnej weryfikacji, pojawianie się i rozpowszechnianie ustaleń, które obalają ich ustalenia, skazując w ten sposób swoją dziedzinę na utrwalanie fałszywych dogmatów. Dowody empiryczne dotyczące opinii ekspertów pokazują, że są one wyjątkowo niewiarygodne[28].
Następstwo 6: Im gorętsza dziedzina nauki (z większą liczbą zaangażowanych zespołów naukowych), tym mniejsze prawdopodobieństwo, że wyniki badań są prawdziwe. To pozornie paradoksalne następstwo wynika z faktu, że jak wspomniano powyżej, PPV pojedynczych odkryć spada, gdy wiele zespołów badaczy jest zaangażowanych w tę samą dziedzinę. Może to wyjaśniać, dlaczego od czasu do czasu obserwujemy duże podekscytowanie, po którym szybko następują poważne rozczarowania w dziedzinach, które przyciągają szeroką uwagę. Przy wielu zespołach pracujących nad tą samą dziedziną i ogromnej ilości danych eksperymentalnych, czas jest najważniejszy w pokonaniu konkurencji. W związku z tym każdy zespół może priorytetowo traktować poszukiwanie i rozpowszechnianie najbardziej imponujących „pozytywnych” wyników. „Negatywne” wyniki mogą stać się atrakcyjne do rozpowszechniania tylko wtedy, gdy inny zespół znalazł „pozytywne” powiązanie w tej samej kwestii. W takim przypadku atrakcyjne może być obalenie twierdzenia przedstawionego w jakimś prestiżowym czasopiśmie. Termin „zjawisko Proteusa” został ukuty w celu opisania tego zjawiska szybko zmieniających się skrajnych twierdzeń badawczych i skrajnie przeciwstawnych obaleń[29]. Dowody empiryczne sugerują, że ta sekwencja skrajnych przeciwieństw jest bardzo powszechna w genetyce molekularnej[29].
[Zjawisko Proteusza jest tendencją w nauce do wczesnych replikacji pracy, które zaprzeczają oryginalnym odkryciom, co jest konsekwencją tendencyjności publikacji. Jest to zjawisko podobne do klątwy zwycięzcy.]
Powyższe następstwa uwzględniają każdy czynnik osobno, ale czynniki te często wpływają na siebie nawzajem. Na przykład badacze pracujący w dziedzinach, w których rzeczywiste rozmiary efektów są postrzegane jako małe, mogą być bardziej skłonni do przeprowadzania dużych badań niż badacze pracujący w dziedzinach, w których rzeczywiste rozmiary efektów są postrzegane jako duże. Uprzedzenia mogą też dominować w gorącej dziedzinie naukowej, dodatkowo podważając wartość predykcyjną wyników badań. Wysoce uprzedzeni interesariusze mogą nawet stworzyć barierę, która powstrzyma wysiłki zmierzające do uzyskania i rozpowszechnienia przeciwstawnych wyników. I odwrotnie, fakt, że dana dziedzina jest gorąca lub występują w niej silnie zainwestowane interesy, może czasami promować większe badania i ulepszone standardy badań, zwiększając wartość predykcyjną wyników badań. Lub masowe testy zorientowane na odkrycia mogą skutkować tak dużą liczbą znaczących związków, że badacze mają wystarczająco dużo do zgłaszania i dalszego wyszukiwania, a tym samym powstrzymują się od pogłębiania danych i manipulacji.
Większość wyników badań jest fałszywa dla większości projektów badawczych i dla większości dziedzin
W opisanych ramach pozytywna wartość predykcyjna [PPV] przekraczająca 50% jest dość trudna do uzyskania. Tabela 4 zawiera wyniki symulacji z wykorzystaniem wzorów opracowanych dla wpływu mocy, stosunku prawdziwych do nieprawdziwych relacji i stronniczości, dla różnych typów sytuacji, które mogą być charakterystyczne dla określonych projektów badań i ustawień. Wnioski z dobrze przeprowadzonego randomizowanego badania kontrolowanego z odpowiednią mocą, rozpoczynającego się od 50% szansy przed badaniem, że interwencja jest skuteczna, są ostatecznie prawdziwe w około 85% przypadków. Dość podobnej wydajności oczekuje się od potwierdzającej metaanalizy dobrej jakości randomizowanych badań: potencjalna stronniczość prawdopodobnie wzrasta, ale moc i szanse przed badaniem są wyższe w porównaniu z pojedynczym randomizowanym badaniem. I odwrotnie, wyniki metaanalizy z niejednoznacznych badań, w których łączenie jest stosowane w celu „skorygowania” niskiej mocy pojedynczych badań, są prawdopodobnie fałszywe, jeśli R ≤ 1:3. Wyniki badań z badań klinicznych o zbyt małej mocy, we wczesnej fazie, byłyby prawdziwe mniej więcej raz na cztery lub nawet rzadziej, jeśli występuje stronniczość. Badania epidemiologiczne o charakterze eksploracyjnym osiągają jeszcze gorsze wyniki, zwłaszcza gdy mają zbyt małą moc, ale nawet badania epidemiologiczne o dobrej mocy mogą mieć tylko jedną na pięć szans na bycie prawdziwymi, jeśli R = 1:10. Wreszcie, w badaniach ukierunkowanych na odkrycia z masowymi testami, w których testowane relacje przekraczają prawdziwe 1000-krotnie (np. 30.000 testowanych genów, z których 30 może być prawdziwymi winowajcami)[30,31], PPV dla każdego deklarowanego związku jest niezwykle niska, nawet przy znacznej standaryzacji metod laboratoryjnych i statystycznych, wyników i ich raportowania w celu zminimalizowania stronniczości.
TABELA 4
PPV wyników badań dla różnych kombinacji mocy (1 – β), stosunku relacji prawdziwych do nieprawdziwych (R) i błędu systematycznego (u)
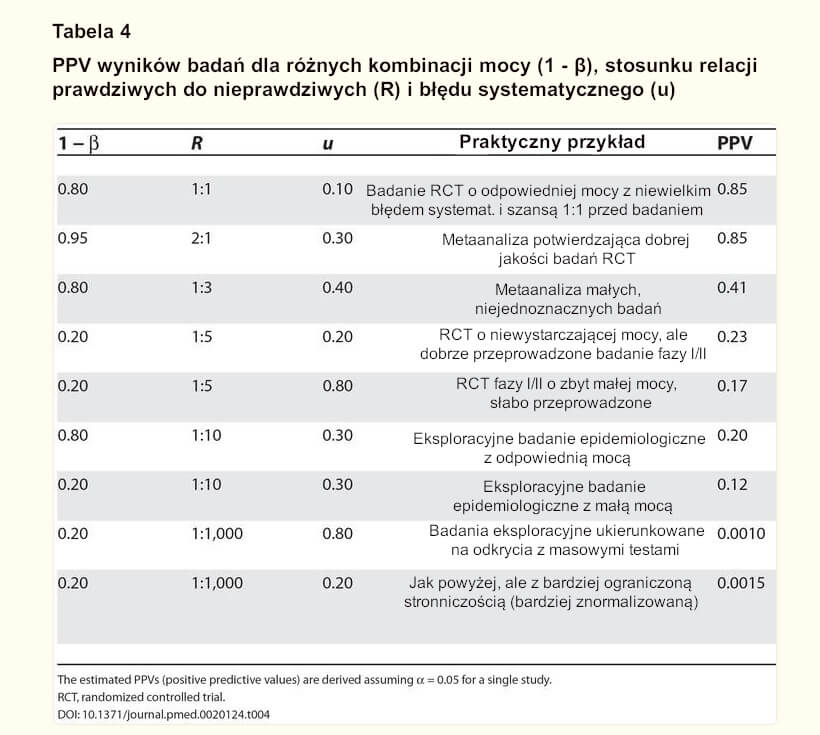
Szacowane PPV (dodatnie wartości predykcyjne) uzyskano przy założeniu a = 0,05 dla pojedynczego badania. RCT, randomizowane badanie kontrolowane.
Twierdzone wyniki badań mogą często być po prostu dokładnymi miarami dominującego uprzedzenia.
Jak wykazano, większość współczesnych badań biomedycznych działa w obszarach o bardzo niskim prawdopodobieństwie prawdziwych odkryć przed i po badaniu. Załóżmy, że w danej dziedzinie badań nie ma żadnych prawdziwych odkryć do odkrycia. Historia nauki uczy nas, że w przeszłości naukowcy często marnowali wysiłki w dziedzinach, które absolutnie nie przyniosły prawdziwych informacji naukowych, przynajmniej w oparciu o nasze obecne zrozumienie. W takim „polu zerowym” idealnie byłoby oczekiwać, że wszystkie zaobserwowane wielkości efektów będą się różnić przypadkowo wokół zera przy braku stronniczości. Zakres, w jakim zaobserwowane wyniki odbiegają od tego, czego można oczekiwać na podstawie samego przypadku, byłby po prostu czystą miarą dominującego uprzedzenia.
Załóżmy na przykład, że żadne składniki odżywcze lub wzorce żywieniowe nie są w rzeczywistości ważnymi czynnikami determinującymi ryzyko rozwoju określonego nowotworu. Załóżmy również, że literatura naukowa zbadała 60 składników odżywczych i twierdzi, że wszystkie z nich są związane z ryzykiem rozwoju tego nowotworu z ryzykiem względnym w zakresie od 1.2 do 1.4 dla porównania górnych i dolnych tercyli spożycia. W takim przypadku deklarowane wielkości efektów są po prostu pomiarem niczego innego, jak stronniczości netto, która była zaangażowana w tworzenie tej literatury naukowej. Twierdzone wielkości efektów są w rzeczywistości najdokładniejszymi szacunkami odchylenia netto. Wynika z tego nawet, że pomiędzy „dziedzinami zerowymi”, dziedziny, które twierdzą, że mają silniejsze efekty (często z towarzyszącymi im twierdzeniami o znaczeniu medycznym lub dla zdrowia publicznego) są po prostu tymi, które utrzymywały najgorsze uprzedzenia.
W przypadku dziedzin o bardzo niskim PPV, kilka prawdziwych związków nie zniekształciłoby zbytnio tego ogólnego obrazu. Nawet jeśli kilka związków jest prawdziwych, kształt rozkładu zaobserwowanych efektów nadal dawałby wyraźną miarę tendencyjności związanej z daną dziedziną. Koncepcja ta całkowicie odwraca sposób, w jaki postrzegamy wyniki badań naukowych. Tradycyjnie badacze postrzegali duże i wysoce znaczące efekty z podekscytowaniem, jako oznaki ważnych odkryć. Zbyt duże i zbyt znaczące efekty mogą być w rzeczywistości bardziej prawdopodobnymi oznakami dużej stronniczości w większości dziedzin współczesnych badań. Powinny one skłonić badaczy do uważnego, krytycznego myślenia o tym, co mogło pójść nie tak z ich danymi, analizami i wynikami.
Oczywiście badacze pracujący w dowolnej dziedzinie prawdopodobnie nie zaakceptują faktu, że cała dziedzina, w której spędzili karierę, jest „dziedziną zerową”. Jednak inne linie dowodowe lub postępy w technologii i eksperymentach mogą ostatecznie doprowadzić do demontażu dziedziny naukowej. Uzyskanie pomiarów stronniczości netto w jednej dziedzinie może być również przydatne do uzyskania wglądu w to, jaki może być zakres stronniczości działającej w innych dziedzinach, w których mogą działać podobne metody analityczne, technologie i konflikty.
Jak możemy poprawić sytuację?
Czy to nieuniknione, że większość wyników badań jest fałszywa, czy też możemy poprawić sytuację? Głównym problemem jest to, że niemożliwe jest ustalenie ze 100% pewnością, jaka jest prawda w jakimkolwiek pytaniu badawczym. Pod tym względem czysty „złoty” standard jest nieosiągalny. Istnieje jednak kilka podejść do poprawy prawdopodobieństwa po badaniu.
Dowody o lepszej mocy, np. duże badania lub metaanalizy o niskiej tendencyjności, mogą być pomocne, ponieważ zbliżają się do nieznanego „złotego” standardu. Duże badania mogą jednak nadal wykazywać tendencyjność, którą należy uznać i której należy unikać. Co więcej, niemożliwe jest uzyskanie dowodów na dużą skalę dla wszystkich milionów i bilionów pytań badawczych stawianych w obecnych badaniach. Dowody na dużą skalę powinny być ukierunkowane na pytania badawcze, w których prawdopodobieństwo przed badaniem jest już znacznie wysokie, tak że znaczące odkrycie badawcze doprowadzi do prawdopodobieństwa po badaniu, które zostanie uznane za dość ostateczne. Dowody na dużą skalę są również szczególnie wskazane, gdy mogą testować główne koncepcje, a nie wąskie, konkretne pytania. Negatywne wyniki mogą wówczas obalić nie tylko konkretne proponowane twierdzenie, ale całą dziedzinę lub jej znaczną część. Wybieranie wyników badań na dużą skalę w oparciu o wąskie kryteria, takie jak promocja marketingowa konkretnego leku, jest w dużej mierze marnowaniem badań. Ponadto należy zachować ostrożność, ponieważ bardzo duże badania mogą być bardziej prawdopodobne, że znajdą formalnie statystycznie istotną różnicę dla trywialnego efektu, który tak naprawdę nie różni się znacząco od zera[32-34].
Po drugie, większość pytań badawczych jest rozwiązywana przez wiele zespołów, a podkreślanie statystycznie istotnych ustaleń jakiegokolwiek pojedynczego zespołu jest mylące. Liczy się całość dowodów. Pomocne może być również zmniejszenie uprzedzeń poprzez wzmocnienie standardów badawczych i ograniczenie uprzedzeń. Może to jednak wymagać zmiany mentalności naukowej, która może być trudna do osiągnięcia. W niektórych projektach badawczych wysiłki mogą być również bardziej skuteczne dzięki wcześniejszej rejestracji badań, np. badań randomizowanych[35]. Rejestracja stanowiłaby wyzwanie dla badań generujących hipotezy. Pewnego rodzaju rejestracja lub tworzenie sieci zbiorów danych lub badaczy w ramach dziedzin może być bardziej wykonalne niż rejestracja każdego eksperymentu generującego hipotezy. Niezależnie od tego, nawet jeśli nie widzimy dużego postępu w rejestracji badań w innych dziedzinach, zasady opracowywania i przestrzegania protokołu mogą być szerzej zapożyczone z randomizowanych badań kontrolowanych.
Wreszcie, zamiast gonić za istotnością statystyczną, powinniśmy lepiej zrozumieć zakres wartości R – szanse przed badaniem – w których działają wysiłki badawcze[10]. Przed przeprowadzeniem eksperymentu badacze powinni rozważyć, jakie są ich zdaniem szanse, że testują prawdziwy, a nie nieprawdziwy związek. Spekulowane wysokie wartości R mogą czasami zostać ustalone. Jak opisano powyżej, o ile jest to etycznie dopuszczalne, duże badania z minimalną stronniczością powinny być przeprowadzane na wynikach badań, które są uważane za względnie ustalone, aby sprawdzić, jak często są one rzeczywiście potwierdzone. Podejrzewam, że kilka uznanych „klasyków” nie przejdzie tego testu[36].
Niemniej jednak większość nowych odkryć będzie nadal wynikać z badań generujących hipotezy o niskim lub bardzo niskim prawdopodobieństwie przed badaniem. Powinniśmy zatem przyznać, że testowanie istotności statystycznej w raporcie z pojedynczego badania daje tylko częściowy obraz, nie wiedząc, ile testów zostało przeprowadzonych poza raportem i w danej dziedzinie w ogóle. Pomimo obszernej literatury statystycznej dotyczącej wielokrotnych korekt testowych[37], zwykle niemożliwe jest rozszyfrowanie, ile pogłębiania danych przez autorów raportu lub inne zespoły badawcze poprzedziło zgłoszone wyniki badań. Nawet gdyby ustalenie tego było możliwe, nie informowałoby nas to o szansach przed badaniem. W związku z tym nieuniknione jest przyjęcie przybliżonych założeń dotyczących tego, ile związków powinno być prawdziwych wśród tych badanych w odpowiednich obszarach badawczych i projektach badawczych. Szersze pole może dostarczyć pewnych wskazówek do oszacowania tego prawdopodobieństwa dla pojedynczego projektu badawczego. Przydatne mogą być również doświadczenia z uprzedzeń wykrytych w innych sąsiednich dziedzinach. Mimo że założenia te byłyby w znacznym stopniu subiektywne, nadal byłyby bardzo przydatne w interpretowaniu twierdzeń badawczych i umieszczaniu ich w kontekście.
Zobacz na: Nauka spod znaku kultu cargo – Richard Feynman [1974]
Odtwarzalność: Tragedia błędów
O stronniczości badań i publikacji finansowanych przez przemysł farmaceutyczny
Nauka™: religia, której nie wolno kwestionować – Henry Gee
Tylko 6% materiałów reklamowych dotyczących leków jest poparte dowodami – Annette Tuffs
Raport pt. Śmierć z powodu medycyny – dr Gary Null, dr Carolyn Dean, dr Martin Feldman, dr Debora Rasio i dr Dorothy Smith. [2003]
COVID – dlaczego terminologia ma znaczenie? – dr Malcolm Kendrick
Redukcja ryzyka względnego na przykładzie 95% skuteczności szczepionek na C-19 – dr Thomas Cowan
Transkrypt filmu pt. Ustawa z 1986 roku
Nowe dane porównujące szczepionych z nieszczepionymi: wskaźnik występowania autyzmu u nieszczepionych wskazuje 1 na 715, a częściowo szczepionych 1 na 440 – Jefferey Jaxen
Szczepieni vs Nieszczepieni: Badanie populacji dzieci nauczanych w systemie edukacji domowej celem zilustrowania zachorowalności – Celeste McGovern
Bibliografia:
1.Ioannidis JP, Haidich AB, Lau J. Any casualties in the clash of randomised and observational evidence? BMJ. 2001;322:879–880.
2. Lawlor DA, Davey Smith G, Kundu D, Bruckdorfer KR, Ebrahim S. Those confounded vitamins: What can we learn from the differences between observational versus randomised trial evidence? Lancet. 2004;363:1724–1727.
3. Vandenbroucke JP. When are observational studies as credible as randomised trials? Lancet. 2004;363:1728–1731.
4. Michiels S, Koscielny S, Hill C. Prediction of cancer outcome with microarrays: A multiple random validation strategy. Lancet. 2005;365:488–492.
5. Ioannidis JPA, Ntzani EE, Trikalinos TA, Contopoulos-Ioannidis DG. Replication validity of genetic association studies. Nat Genet. 2001;29:306–309.
6. Colhoun HM, McKeigue PM, Davey Smith G. Problems of reporting genetic associations with complex outcomes. Lancet. 2003;361:865–872.
7. Ioannidis JP. Genetic associations: False or true? Trends Mol Med. 2003;9:135–138.
8. Ioannidis JPA. Microarrays and molecular research: Noise discovery? Lancet. 2005;365:454–455.
9. Sterne JA, Davey Smith G. Sifting the evidence—What’s wrong with significance tests. BMJ. 2001;322:226–231.
10.Wacholder S, Chanock S, Garcia-Closas M, Elghormli L, Rothman N. Assessing the probability that a positive report is false: An approach for molecular epidemiology studies. J Natl Cancer Inst. 2004;96:434–442.
11. Risch NJ. Searching for genetic determinants in the new millennium. Nature. 2000;405:847–856.
12. Kelsey JL, Whittemore AS, Evans AS, Thompson WD. Methods in observational epidemiology, 2nd ed. New York: Oxford U Press; 1996. 432 pp.
13. Topol EJ. Failing the public health—Rofecoxib, Merck, and the FDA. N Engl J Med. 2004;351:1707–1709.
14. Yusuf S, Collins R, Peto R. Why do we need some large, simple randomized trials? Stat Med. 1984;3:409–422.
15. Altman DG, Royston P. What do we mean by validating a prognostic model? Stat Med. 2000;19:453–473.
16. Taubes G. Epidemiology faces its limits. Science. 1995;269:164–169.
17. Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, et al. Molecular classification of cancer: Class discovery and class prediction by gene expression monitoring. Science. 1999;286:531–537.
18. Moher D, Schulz KF, Altman DG. The CONSORT statement: Revised recommendations for improving the quality of reports of parallel-group randomised trials. Lancet. 2001;357:1191–1194.
19. Ioannidis JP, Evans SJ, Gotzsche PC, O’Neill RT, Altman DG, et al. Better reporting of harms in randomized trials: An extension of the CONSORT statement. Ann Intern Med. 2004;141:781–788.
20. International Conference on Harmonisation E9 Expert Working Group. ICH Harmonised Tripartite Guideline. Statistical principles for clinical trials. Stat Med. 1999;18:1905–1942.
21. Moher D, Cook DJ, Eastwood S, Olkin I, Rennie D, et al. Improving the quality of reports of meta-analyses of randomised controlled trials: The QUOROM statement. Quality of Reporting of Meta-analyses. Lancet. 1999;354:1896–1900.
22. Stroup DF, Berlin JA, Morton SC, Olkin I, Williamson GD, et al. Meta-analysis of observational studies in epidemiology: A proposal for reporting. Meta-analysis of Observational Studies in Epidemiology (MOOSE) group. JAMA. 2000;283:2008–2012.
23. Marshall M, Lockwood A, Bradley C, Adams C, Joy C, et al. Unpublished rating scales: A major source of bias in randomised controlled trials of treatments for schizophrenia. Br J Psychiatry. 2000;176:249–252.
24. Altman DG, Goodman SN. Transfer of technology from statistical journals to the biomedical literature. Past trends and future predictions. JAMA. 1994;272:129–132.
25. Chan AW, Hrobjartsson A, Haahr MT, Gotzsche PC, Altman DG. Empirical evidence for selective reporting of outcomes in randomized trials: Comparison of protocols to published articles. JAMA. 2004;291:2457–2465.
26. Krimsky S, Rothenberg LS, Stott P, Kyle G. Scientific journals and their authors’ financial interests: A pilot study. Psychother Psychosom. 1998;67:194–201.
27. Papanikolaou GN, Baltogianni MS, Contopoulos-Ioannidis DG, Haidich AB, Giannakakis IA, et al. Reporting of conflicts of interest in guidelines of preventive and therapeutic interventions. BMC Med Res Methodol. 2001;1:3.
28. Antman EM, Lau J, Kupelnick B, Mosteller F, Chalmers TC. A comparison of results of meta-analyses of randomized control trials and recommendations of clinical experts. Treatments for myocardial infarction. JAMA. 1992;268:240–248.
29. Ioannidis JP, Trikalinos TA. Early extreme contradictory estimates may appear in published research: The Proteus phenomenon in molecular genetics research and randomized trials. J Clin Epidemiol. 2005;58:543–549.
30. Ntzani EE, Ioannidis JP. Predictive ability of DNA microarrays for cancer outcomes and correlates: An empirical assessment. Lancet. 2003;362:1439–1444.
31. Ransohoff DF. Rules of evidence for cancer molecular-marker discovery and validation. Nat Rev Cancer. 2004;4:309–314.
32. Lindley DV. A statistical paradox. Biometrika. 1957;44:187–192.
33. Bartlett MS. A comment on D.V. Lindley’s statistical paradox. Biometrika. 1957;44:533–534.
34. Senn SJ. Two cheers for P-values. J Epidemiol Biostat. 2001;6:193–204.
35. De Angelis C, Drazen JM, Frizelle FA, Haug C, Hoey J, et al. Clinical trial registration: A statement from the International Committee of Medical Journal Editors. N Engl J Med. 2004;351:1250–1251.
36. Ioannidis JPA. Contradicted and initially stronger effects in highly cited clinical research. JAMA. 2005;294:218–228.
37. Hsueh HM, Chen JJ, Kodell RL. Comparison of methods for estimating the number of true null hypotheses in multiplicity testing. J Biopharm Stat. 2003;13:675–689.